Arte azteca › Civiltà Azteca › La storia egiziana di Cenerentola smascherata » Origini e Storia
Articoli e definizioni › Contenuto
- Arte azteca › origini
- Civiltà Azteca › origini
- La storia egiziana di Cenerentola smascherata › origini
Civiltà antiche › Luoghi storici e i loro personaggi
Arte azteca › origini
Definizione e origini

L' impero azteco, centrato nella capitale di Tenochtitlan, dominava la maggior parte della Mesoamerica nel XV e XVI secolo CE. Con la conquista militare e l'espansione commerciale anche l'arte degli Aztechi si diffuse, aiutando gli Aztechi a raggiungere un'egemonia culturale e politica sui loro sudditi e creando per i posteri una testimonianza tangibile dell'immaginazione artistica e del grande talento degli artisti di quest'ultima grande civiltà mesoamericana.
INFLUENZE
Fili comuni attraversano la storia dell'arte mesoamericana. Le civiltà olmeca, maya, tolteca e zapotese, tra le altre, perpetuavano una tradizione artistica che mostrava l'amore per la scultura monumentale in pietra, l'architettura imponente, la ceramica altamente decorata, i timbri geometrici per tessuti e body art e la lavorazione del metallo mozzafiato a cui erano abituati rappresentano persone, animali, piante, divinità e caratteristiche della cerimonia religiosa, specialmente quei riti e divinità legate alla fertilità e all'agricoltura.
Gli artisti aztechi sono stati influenzati anche dai loro contemporanei degli stati confinanti, in particolare artisti di Oaxaca (alcuni dei quali risiedevano permanentemente a Tenochtitlan) e la regione di Huastec della costa del Golfo, dove esisteva una forte tradizione di scultura tridimensionale. Queste diverse influenze e gli stessi gusti e ammirazione eclettici degli antichi Atzechi facevano della loro arte una delle più svariate culture antiche ovunque. Sculture di dèi raccapriccianti con immagini astratte potrebbero provenire dallo stesso laboratorio di opere naturalistiche che rappresentavano la bellezza e la grazia della forma animale e umana.
CARATTERISTICHE DELL'ARTE AZTEC
La lavorazione dei metalli era un'abilità particolare degli Aztechi. Il grande artista rinascimentale Albrecht Drurer ha visto alcuni dei manufatti riportati in Europa che gli hanno fatto dire: "... Non ho mai visto in tutti i miei giorni ciò che tanto ha esaltato il mio cuore, come queste cose. Poiché vidi tra loro stupendi oggetti artistici e mi meravigliai della sottile ingenuità degli uomini in queste terre lontane ". Sfortunatamente, come con la maggior parte degli altri artefatti, questi oggetti sono stati fusi per la valuta, e così pochi esempi sopravvivono alle raffinate abilità dei metalli aztechi in oro e argento. Sono stati scoperti oggetti più piccoli, tra i quali labrets in oro (piercing alle labbra), ciondoli, anelli, orecchini e collane in oro che rappresentano di tutto, dalle aquile alle conchiglie alle divinità, che testimoniano l'abilità nella fusione a cera persa e il lavoro a filigrana del artigiani più raffinati o tolteca.
GLI AZTECS DIALOGANO ANCHE L'ARTE COME STRUMENTO PER RAFFORZARE LA LORO DOMINANZA MILITARE E CULTURALE ATTRAVERSO MESOAMERICA.
La scultura azteca è stata una migliore sopravvissuta, e il suo soggetto era molto spesso individui appartenenti alla vasta famiglia di dei che essi adoravano. Scolpiti nella pietra e nel legno queste figure, a volte di dimensioni monumentali, non erano idoli che contenevano lo spirito del dio, poiché nella religione azteca si pensava che lo spirito di una particolare divinità risiedesse in fasci sacri custoditi nei santuari e nei templi. Tuttavia, si pensava che fosse necessario "nutrire" queste sculture con sangue e oggetti preziosi, quindi racconti dai conquistatori spagnoli di enormi statue imbrattate di sangue e tempestate di gioielli e oro. Altre grandi sculture, più a tutto tondo, includono il magnifico dio seduto Xochipilli e i vari chacmools, figure reclinate con una cavità scolpita nel petto che era usata come ricettacolo per i cuori delle vittime sacrificali. Questi, come la maggior parte delle altre sculture azteche, sarebbero stati dipinti una volta con un'ampia gamma di colori vivaci.
Sculture di piccole dimensioni sono state trovate nei siti del Messico centrale. Questi spesso prendono la forma di divinità locali e in particolare di divinità legate all'agricoltura. Le più comuni sono figure femminili erette di una divinità del mais, in genere con un copricapo impressionante, e il dio del mais Xipe Totec. Mancando della finezza dell'arte imperiale, queste sculture e simili figure di ceramiche rappresentano spesso il lato più benevolo degli dei aztechi.

Coltello cerimoniale azteco
Il lavoro in miniatura era anche popolare dove soggetti come piante, insetti e conchiglie venivano resi in materiali preziosi come la corniola, la perla, l'ametista, il cristallo di rocca, l'ossidiana, il guscio e il più prezioso di tutti i materiali, la giada. Un altro materiale molto apprezzato erano le piume esotiche, in particolare il piumaggio verde dell'uccello quetzal. Piume tagliate a pezzetti erano usate per creare dipinti a mosaico, come decorazioni per scudi, costumi e ventilatori, e in magnifici copricapo come quello attribuito a Motecuhzoma II, che ora si trova nel Museum für Völkerkunde a Vienna.
Il turchese era un materiale particolarmente amato dagli artisti aztechi e l'uso di esso in forma di mosaico per coprire sculture e maschere ha creato alcune delle immagini più impressionanti della Mesoamerica. Un tipico esempio è il teschio umano decorato che rappresenta il dio Tezcatlipoca e che ora risiede nel British Museum, a Londra. Un altro bell'esempio è la maschera di Xiuhtecuhtli, il dio del fuoco, con occhi di madreperla dall'aspetto assonnato e una serie perfetta di denti di conchiglia bianca. Infine, c'è il magnifico pettorale a due teste di serpente, ora anche nel British Museum. Con il legno di cedro scolpito completamente ricoperto di piccoli quadrati di turchese e le bocche rosse e i denti bianchi resi rispettivamente in spondylus e conchiglia, il pezzo era probabilmente una volta parte di un costume da cerimonia. Il serpente era un'immagine potente nell'arte azteca in quanto la creatura, in grado di liberarsi della pelle, rappresentava la rigenerazione ed era anche particolarmente associata al dio Quetzalcoatl.
Nonostante l'assenza della ruota del vasaio, gli Aztechi erano anche abili con la ceramica, come indicato da grandi figure cave e da diverse urne con coperchio splendidamente scolpite che furono scavate dal lato del Templo Mayor a Tenochtitlan, probabilmente usate come ricettacoli per le ceneri funerarie. Altri esempi di lavori in ceramica sono gli incensieri modellati con gambe a treppiede di Texcoco, brocche con beccuccio e eleganti tazze a forma di clessidra. Questi vasi sono tipicamente a parete sottile, ben proporzionati, hanno una colorazione crema o rossa e nera, e portano disegni geometrici finemente dipinti in disegni precedenti e flora e fauna negli esempi successivi. Le ceramiche più pregiate dagli stessi Aztechi, e il tipo usato da Motecuhzoma, erano gli articoli ultrasottili di Cholula di Cholollan nella Valle di Puebla. I vasi potevano anche essere fatti da stampi o intagliati mentre l'argilla era ancora dura come la pelle. Un bell'esempio di questi vasi antropomorfi è il celebre vaso raffigurante la testa del dio della pioggia Tlaloc dipinto di un blu brillante, con gli occhi da maschera e le temibili zanne rosse, ora nel Museo Nazionale di Antropologia a Città del Messico.

Tlaloc
Gli strumenti musicali erano un'altra parte importante del repertorio dell'artista azteco. Questi includono flauti in ceramica e teponaztlis e huehuetl in legno, rispettivamente, tamburi cerimoniali lunghi e retti. Sono riccamente decorati con intagli, e uno dei più belli è il tamburo di Malinalco che è ricoperto da danzatori e aquile che rappresentano vittime sacrificali come indicato da striscioni e rotoli di parole di simboli di guerra e di fuoco.
ARTE COME PROPAGANDA
Gli Aztechi, come i loro predecessori culturali, usavano l'arte come strumento per rafforzare il loro dominio militare e culturale.Imponendo edifici, affreschi, sculture e persino manoscritti, specialmente in siti chiave come Tenochtitlan, non solo hanno rappresentato e persino replicato gli elementi chiave della religione azteca, ma hanno anche ricordato ai popoli soggetti la ricchezza e il potere che hanno permesso la loro costruzione e produzione.
L'esempio supremo di questo uso dell'arte come trasportatore di messaggi politici e religiosi è il Templo Mayor di Tenochtitlan che era molto più di una piramide enormemente impressionante. È stato accuratamente progettato in ogni dettaglio per rappresentare la sacra montagna di serpenti della terra di Coatepec, così importante nella religione e nella mitologia azteca.Questa montagna era il luogo in cui Coatlicue (la terra) diede alla luce suo figlio Huitzilopochtli (il sole), che sconfisse gli altri dei (le stelle) guidati dalla sorella Coyolxauhqui (la luna). Un tempio di Huitzilopochtli fu costruito sulla cima della piramide insieme ad un altro in onore del dio della pioggia Tlaloc. Ulteriori associazioni con il mito sono le sculture di serpenti che rivestono la base e la grande pietra di Coyolxauhqui scolpita nel c. 1473 CE, trovato anche alla base della piramide e che rappresenta in rilievo il corpo smembrato della dea caduta. La pietra, insieme ad altre sculture come la Pietra di Tizoc, collegava questo immaginario cosmico alla sconfitta contemporanea dei nemici locali. Nel caso della pietra di Coyolxauhqui, si fa riferimento alla sconfitta del Tlatelolca. Infine, il Templo Mayor era di per sé un deposito di arte in quanto, una volta esplorato il suo interno, una vasta schiera di oggetti d'arte e di scultura furono scoperti sepolti con i resti dei morti e questi pezzi sono, in molti casi, opere che gli Aztechi avevano raccolti da culture più antiche della loro.
Anche i templi che esaltavano la visione azteca del mondo erano costruiti nei territori conquistati. Di solito gli Aztechi lasciavano le strutture politiche e amministrative esistenti, ma imponevano le loro divinità in una gerarchia al di sopra delle divinità locali, e ciò avveniva in gran parte attraverso l'architettura e l'arte, sostenute da cerimonie sacrificali in questi nuovi luoghi sacri, tipicamente costruite su precedenti siti sacri e spesso in ambienti spettacolari come sulle cime delle montagne.
Le immagini azteche che si estendono attraverso l' impero includono molte divinità meno conosciute di Huitzilopochtli e ci sono un numero sorprendente di esempi di dèi naturali e agricoli. Forse i più famosi sono i rilievi della dea dell'acqua Chalchiuhtlicue sulla collina Malinche nei pressi dell'antica Tula. Queste e altre opere di arte azteca erano spesso realizzate da artisti locali e potrebbero essere state commissionate da autorità che rappresentano lo stato o da coloni privati del cuore azteco. L'arte architettonica, le incisioni rupestri di divinità, animali e scudi e altri oggetti d'arte sono stati trovati in tutto l'impero da Puebla a Veracruz e in particolare intorno a città, colline, sorgenti e grotte. Inoltre, queste opere sono solitamente uniche, suggerendo l'assenza di laboratori organizzati.

Tizoc Stone
CAPOLAVORI
La grande pietra circolare di Tizoc (scolpita nel 1485 CE dal basalto) è un mix magistrale di mitologia cosmica e politica del mondo reale. Originariamente era usato come superficie su cui compiere sacrifici umani e poiché queste vittime erano di solito guerrieri sconfitti, è del tutto appropriato che i rilievi intorno al bordo della pietra raffigurino il sovrano azteco Tizoc che attacca i guerrieri della Matlatzinca, un'area conquistata da Tizoc alla fine del XV secolo CE. I vinti sono anche raffigurati come Chichimec, cioè barbari senza terra, mentre i vincitori indossano il vestito nobile del venerato antico Toltec. La superficie superiore della pietra, di 2,67 m di diametro, raffigura un disco solare a otto punte. La Pietra di Tizoc risiede ora nel Museo Nazionale di Antropologia a Città del Messico.

Coatlicue
La massiccia statua di basalto di Coatlicue (scolpita nell'ultimo mezzo secolo di dominio azteco) è ampiamente considerata uno dei migliori esempi di scultura azteca. La dea è presentata in forma terrificante con due teste di serpente, piedi e mani artigliate, una collana di mani smembrate e cuori umani con un ciondolo a forma di teschio e una gonna di serpenti contorti.Forse uno di un gruppo di quattro e che rappresenta la rivelazione del potere femminile e del terrore, la statua alta 3,5 m si sporge leggermente in avanti in modo che l'effetto drammatico complessivo del pezzo sia così emotivo che è comprensibile il motivo per cui la statua è stata effettivamente ri-sepolta diversi tempi successivi allo scavo originale del 1790 d.C. La statua di Coatlicue ora risiede nel Museo Nazionale di Antropologia a Città del Messico.

Aztec Sun Stone
The Sun Stone, noto anche come Calendar Stone (nonostante non sia un calendario funzionante), deve essere l'oggetto d'arte più riconoscibile prodotto da una qualsiasi delle grandi civiltà della Mesoamerica. Scoperto nel XVIII secolo vicino alla cattedrale di Città del Messico, la pietra è stata scolpita c. 1427 CE e mostra un disco solare che presenta i cinque mondi consecutivi del sole della mitologia azteca. La pietra di basalto ha un diametro di 3,78 m, quasi un metro di spessore e faceva parte del complesso Templo Mayor di Tenochtitlan. Al centro della pietra c'è una rappresentazione del dio sole Tonatiuh (il Sole del giorno) o Yohualtonatiuh (il Sole della notte) o il mostro della terra primordiale Tlaltecuhtli, in quest'ultimo caso che rappresenta la distruzione finale del mondo quando cadde il 5 ° sole alla terra. Intorno alla faccia centrale in quattro punti ci sono gli altri quattro soli che successivamente si sono sostituiti dopo che gli dei Quetzalcoatl e Tezcatlipoca hanno lottato per il controllo del cosmo fino all'era del 5 ° sole. Ai lati della faccia centrale ci sono due teste o zampe di giaguaro, ognuna con un cuore che rappresenta il regno terrestre. Le due teste in basso al centro rappresentano serpenti di fuoco, ei loro corpi corrono lungo il perimetro della pietra con ogni estremità in una coda. Anche i quattro punti cardinali e le direzioni inter-cardinali sono indicati rispettivamente con punti più grandi e minori.
Come ultimo esempio della ricchezza dell'arte azteca che è sopravvissuta ai migliori sforzi distruttivi dei loro conquistatori, c'è il guerriero aquilotto di Tenochtitlan, a grandezza naturale. La figura, che sembra sul punto di spiccare il volo, è in terracotta ed è stata realizzata in quattro pezzi separati. Questo cavaliere dell'Aquila indossa un elmo che rappresenta il rapace, ha le ali e persino i piedi artigliati. Resti di stucco suggeriscono che la figura fosse una volta ricoperta di piume vere per un effetto ancora più simile alla vita. Originariamente, sarebbe stato in piedi con un partner, su entrambi i lati di una porta.
CONCLUSIONE
Dopo la caduta dell'impero azteco, la produzione di arte indigena andò in declino. Tuttavia, alcuni progetti aztechi vivevano nel lavoro di artisti locali impiegati dai frati agostiniani per decorare le loro nuove chiese durante il XVI secolo. Manoscritti e pitture di piume continuarono a essere prodotti, ma fu solo alla fine del XVIII secolo che un interesse per l'arte e la storia precolombiana portò a un'indagine più sistematica su ciò che stava sotto le fondamenta delle moderne città messicane.Lentamente, un numero sempre crescente di artefatti aztechi ha rivelato, nel caso non ci fosse mai stato alcun dubbio, prove probanti che gli Aztechi fossero tra gli artisti più ambiziosi, creativi ed eclettici che la Mesoamerica avesse mai prodotto.
Civiltà Azteca › origini
Definizione e origini
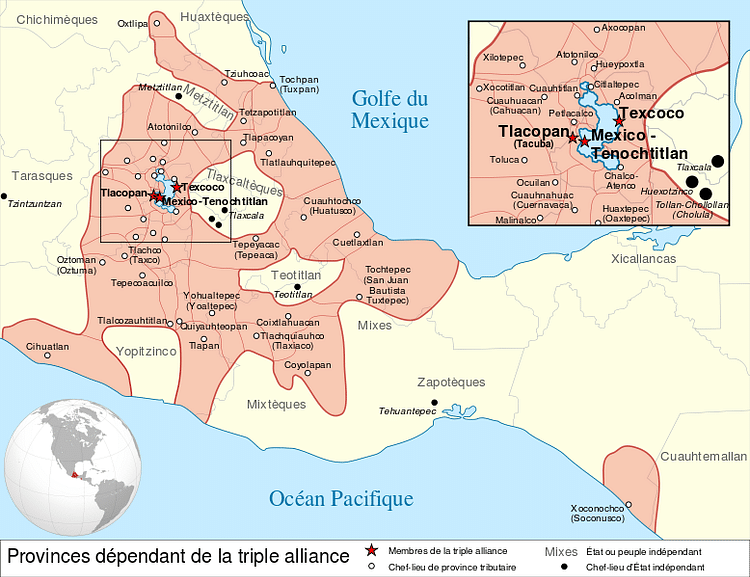
L' impero azteco prosperò tra c. 1345 e 1521 CE e, nella sua massima estensione, copriva la maggior parte del Mesoamerica settentrionale. I guerrieri aztechi riuscirono a dominare i loro stati vicini e permisero a governanti come Motecuhzoma II di imporre ideali e religione azteca attraverso il Messico. Ben compiuta nell'agricoltura e nel commercio, l'ultima delle grandi civiltà mesoamericane si distinse anche per la sua arte e architettura, che è tra le migliori mai prodotte nel continente.
Lo stato azteco è in realtà la civiltà mesoamericana più ben documentata con fonti che includono archeologia, libri nativi (codici) e resoconti lunghi e dettagliati dei loro conquistatori spagnoli - sia da militari che da religiosi cristiani. Queste ultime fonti potrebbero non essere sempre affidabili, ma il quadro che abbiamo degli Aztechi, delle loro istituzioni, delle pratiche religiose, della guerra e della vita quotidiana è ricco e continua ad essere costantemente ampliato con l'aggiunta di dettagli attraverso gli sforzi degli archeologi del 21 ° secolo. e studiosi.
PANORAMICA STORICA
A partire dal 1100 d.C. le città-stato o altepetl che si estendevano nel Messico centrale cominciarono a competere tra loro per le risorse locali e il dominio regionale. Ogni stato aveva il suo sovrano o tlatoani che guidava un consiglio di nobili, ma questi piccoli centri urbani circondati da terreni agricoli cercarono presto di espandere la loro ricchezza e influenza in modo che entro il c. 1400 CE diversi piccoli imperi si erano formati nella Valle del Messico. Dominanti tra questi erano Texcoco, capitale della regione Acholhua, e Azcapotzalco, capitale del Tepenec. Questi due imperi si trovarono faccia a faccia nel 1428 DC con la guerra Tepanec. Le forze di Azcapotzalco furono sconfitte da un'alleanza tra Texcoco, Tenochtitlan (la capitale dei Mexica) e diverse altre città minori. Dopo la vittoria si formò una tripla alleanza tra Texcoco, Tenochtitlan e una città ribelle Tepanec, Tlacopan. Una campagna di espansione territoriale iniziò dove il bottino di guerra - di solito sotto forma di tributi dai conquistati - era condiviso tra queste tre grandi città. Nel corso del tempo Tenochtitlan arrivò a dominare l'Alleanza, il suo sovrano divenne il supremo ruoter - il huey tlatoque ('re supremo') - e la città si affermò come la capitale dell'impero azteco.
I MAESTRI DEL MONDO, IL LORO IMPERO SONO COSIENTI E ABBONDANTI CHE AVEVANO CONQUISTATO TUTTE LE NAZIONI. DIEGO DURÁN
L'impero continuò ad espandersi dal 1430 EV e l'esercito azteco - sostenuto dalla coscrizione di tutti i maschi adulti, uomini forniti da stati alleati e conquistati, e gruppi di élite come i guerrieri Aquila e Jaguar - spazzò via i loro rivali. I guerrieri aztechi indossavano armature di cotone imbottite, portavano uno scudo di legno o di canne coperto di pelle e impugnavano armi come una spada affilata ( macuahuitl ), una lancia o un lanciatore di dardi ( atlatl ) e arco e frecce. Anche i guerrieri d'élite indossavano spettacolari costumi di pelle e piume e costumi per indicare il loro grado. Le battaglie erano concentrate nelle o intorno alle grandi città e quando questi cadevano i vincitori reclamavano l'intero territorio circostante. Furono estratti regolari tributi e i prigionieri furono riportati a Tenochtitlan per il sacrificio rituale. In questo modo l'impero azteco arrivò a coprire la maggior parte del Messico settentrionale, un'area di circa 135.000 chilometri quadrati.
L'impero fu tenuto insieme attraverso la nomina di funzionari del cuore azteco, matrimoni misti, donazioni, inviti a cerimonie importanti, la costruzione di monumenti e opere d'arte che promuovevano l'ideologia imperiale azteca e, soprattutto, l'onnipresente minaccia di intervento militare. Alcuni stati furono integrati più di altri mentre quelli sulle estremità dell'impero divennero utili zone cuscinetto contro i vicini più ostili, in particolare la civiltà Tarasciana.
Tenochtitlán
La capitale azteca di Tenochtitlan, sulla sponda occidentale del Lago di Texcoco, fiorì in modo che la città potesse vantare almeno 200.000 abitanti all'inizio del XVI secolo, diventando così la città più grande delle Americhe precolombiane. Questi abitanti erano divisi in diversi strati sociali. In cima c'erano i sovrani locali ( teteuhctin ), poi nobili ( pipiltin ), popolani ( macehualtin ), servi della gleba ( mayeque ) e infine schiavi ( tlacohtin ). Gli strati sembrano essere stati relativamente fissi, ma ci sono alcune prove di movimento tra di loro, specialmente nelle classi inferiori.

Temple Mayor, Tenochtitlan
Non solo la capitale politica e religiosa, Tenochtitlán era anche un enorme centro commerciale con merci che scorrevano dentro e fuori come oro, greenstone, turchese, cotone, fagioli di cacao, tabacco, ceramica, utensili, armi, generi alimentari (tortillas, salse cile, mais, fagioli e persino insetti, per esempio) e schiavi. Gli invasori spagnoli furono enormemente colpiti dallo splendore della città e dalle magnifiche architetture e opere d'arte, in particolare la piramide del Templo Mayor e le massicce sculture in pietra. A dominare la città c'era l'enorme Sacro Recinto con i suoi templi e la sua monumentale pista da ballo. Anche la gestione delle acque di Tenochtitlan era impressionante, con grandi canali che attraversavano la città, circondata anch'essa da chinampas, campi allagati e allagati, che aumentarono notevolmente la capacità agricola degli Aztechi. C'erano anche argini anti-alluvione, bacini artificiali per l'acqua dolce e meravigliosi giardini fioriti sparsi per la città.
L'intera città è stata progettata per ispirare soggezione nella gente, in particolare visitando i nobili che, intrattenuti con sontuose cerimonie, potevano vedere che i Mexica Aztechi erano veramente:
Maestri del mondo, il loro impero così vasto e abbondante che avevano conquistato tutte le nazioni e che tutti erano i loro vassalli. Gli ospiti, vedendo tale ricchezza e opulenza e tale autorità e potere, erano pieni di terrore.(Diego Durán, il frate spagnolo, citato in Nichols, 451)
RELIGIONE
Mitologia e religione, come nella maggior parte delle culture antiche, erano strettamente intrecciate con gli Aztechi. La vera fondazione di Tenochtitlán era basata sulla convinzione che i popoli della mitica terra dell'abbondanza di Aztlán (letteralmente "Terra degli aironi bianchi" e origine del nome azteco) nel lontano nord-ovest si erano stabiliti per la prima volta nella Valle del Messico. Erano stati mostrati come il loro dio Huitzilopochtli che aveva inviato un'aquila seduta su un cactus per indicare esattamente dove questi migranti avrebbero dovuto costruire la loro nuova casa. Il dio diede anche a queste persone il loro nome, i Mexica, che insieme ad altri gruppi etnici, che parlavano in modo simile a Nahuatl, costituirono collettivamente i popoli ora generalmente conosciuti come gli Aztechi.
Il pantheon azteco comprendeva un misto di antiche divinità mesoameriane e in particolare divinità messicane. I due principali dei adorati erano Huitzilopochtli (la guerra e il dio del sole) e Tlaloc (il dio della pioggia) ed entrambi avevano un tempio in cima alla piramide Templo Mayor nel cuore di Tenochtitlan. Altre divinità importanti erano Quetzalcoatl (il dio serpente piumato comune a molte culture mesoamericane), Tezcatlipoca (dio supremo di Texcoco), Xipe Totec (dio della primavera e dell'agricoltura), Xiuhtecuhtli (dio del fuoco), Xochipilli (dio dell'estate e dei fiori), Ometeotl (il dio creatore), Mictlantecuhtli(dio dei morti) e Coatlicue (la dea madre terra).

Quetzalcoatl
Questa schiera di divinità a volte sconcertante presiede a ogni aspetto della condizione umana. Il calendario delle cerimonie in onore di queste divinità era dettato da una varietà di calendari. C'era il calendario azteco di 260 giorni diviso in 20 settimane, ciascuna di 13 giorni che portava nomi come Coccodrillo e Vento. C'era anche un calendario solare composto da 18 mesi, ciascuno di 20 giorni. Anche il periodo di 584 giorni che copriva l'ascesa di Venere era importante e c'era un ciclo di sole di 52 anni da considerare. Il movimento dei pianeti e delle stelle è stato attentamente osservato (anche se non con la stessa accuratezza, come avevano fatto i Maya ) e hanno fornito il motivo per i tempi specifici di molti riti religiosi e pratiche agricole.
Il sole, non a caso, ha avuto un grande significato per gli Aztechi. Credevano che il mondo attraversasse una serie di secoli cosmici, ognuno avesse il suo sole, ma alla fine ogni mondo fu distrutto e sostituito da un altro fino a raggiungere la quinta ed ultima età - l'attuale giorno per gli Aztechi. Questa progressione cosmica è stata meravigliosamente rappresentata nella famosa Pietra del Sole, ma anche in molti altri luoghi.
Gli dei erano onorati di feste, banchetti, musica, danze, decorazioni di statue, incenso di incenso, sepoltura rituale di beni preziosi, penitenze come il sangue e sacrifici di animali. Gli esseri umani, sia gli adulti che meno spesso i bambini, venivano spesso sacrificati per "nutrire" metaforicamente gli dei e tenerli felici affinché non si arrabbiassero e rendessero la vita difficile agli umani inviando tempeste, siccità ecc. O anche solo per mantenere il sole che appariva ogni giorno. Le vittime venivano solitamente prese dalla parte perdente nelle guerre. In effetti, le cosiddette "Guerre fiorite" furono intraprese specificamente per raccogliere vittime sacrificali. Le offerte più prestigiose erano quei guerrieri che avevano mostrato grande coraggio in battaglia. Il sacrificio stesso poteva assumere tre forme principali: il cuore veniva rimosso, la vittima veniva decapitata, o la vittima veniva costretta a combattere in una disperata lotta unilaterale contro guerrieri d'élite. C'erano anche imitatori che indossavano le insegne di un dio specifico e al culmine della cerimonia venivano sacrificati.

Xochipilli
ARCHITETTURA E ARTE
Gli Aztechi apprezzavano le belle arti e raccoglievano pezzi provenienti da tutto il loro impero per essere riportati a Tenochtitlán e spesso sepolti in modo cerimoniale. L'arte azteca non era nulla se non eclettica e spaziava da oggetti preziosi in miniatura incisi a massicci templi in pietra. Le sculture monumentali erano particolarmente favorite e potevano essere mostruose mostruosità come la colossale statua Coatlicue o essere molto realistiche come la famosa scultura di un Xochipilli seduto.
Organizzati in corporazioni e attaccati ai palazzi principali, gli artigiani potevano specializzarsi nella lavorazione dei metalli, nell'intaglio del legno o nella scultura in pietra, con materiali usati come l'ametista, il cristallo di rocca, l'oro, l' argento e le piume esotiche. Forse alcuni degli oggetti d'arte più sorprendenti sono quelli che impiegavano il mosaico turchese come la famosa maschera di Xuihtecuhtli. Forme comuni di vasi di ceramica includono vasi antropomorfi in colori vivaci e di speciale nota è stata la ceramica Cholula finemente preparata e molto pregiata di Cholollan.
L'arte azteca raffigurava tutti i tipi di soggetti, ma soprattutto erano popolari animali, piante e divinità, in particolare quelli legati alla fertilità e all'agricoltura. L'arte potrebbe anche essere usata come propaganda per diffondere il dominio imperiale di Tenochtitlan. Esempi come la Pietra del Sole, la Pietra di Tizoc e il Trono di Motecuhzoma II ritraggono tutti l'ideologia azteca e cercano di correlare strettamente i governanti politici con gli eventi cosmici e persino con gli stessi dei. Anche l'architettura potrebbe raggiungere questo scopo, ad esempio, la piramide Templo Mayor ha cercato di replicare la sacra montagna di serpenti della mitologia azteca, Coatepec, e templi e statue con simboli aztechi sono stati installati in tutto l'impero.
CROLLO
L'impero azteco, che controllava circa 11.000.000 di persone, aveva sempre avuto a che fare con piccole ribellioni - in genere, quando i nuovi governanti prendevano il potere a Tenochtitlan - ma questi erano sempre stati rapidamente schiacciati. La marea cominciò a girare, tuttavia, quando gli Aztechi furono pesantemente sconfitti dai Tlaxcala e Huexotzingo nel 1515 CE.Con l'arrivo degli spagnoli, alcuni di questi stati ribelli avrebbero di nuovo cogliere l'opportunità per ottenere la loro indipendenza. Quando finalmente i conquistadores arrivarono dal Vecchio Mondo navigando i loro palazzi galleggianti e guidati da Hernán Cortés, i loro primi rapporti con il capo degli Aztechi, Motecuhzoma II, furono amichevoli e furono scambiati doni preziosi. Le cose andarono male, quando un piccolo gruppo di soldati spagnoli fu ucciso a Tenochtitlan mentre Cortés era lontano a Veracruz. I guerrieri aztechi, infelici per la passività di Motecuhzoma, lo rovesciarono e imposero Cuitlahuac come nuovo tlatoani. Questo incidente fu proprio ciò di cui Cortés aveva bisogno e tornò in città per alleviare lo spagnolo assediato rimasto, ma fu costretto a ritirarsi il 30 giugno 1520 CE in quella che divenne nota come la Noche Triste. Radunando gli alleati locali, Cortés tornò dieci mesi dopo e nel 1521 CE assediò la città. Mancando di cibo e devastato dalle malattie, gli Aztechi, ora guidati da Cuauhtemoc, alla fine crollarono nel fatidico giorno del 13 agosto 1521 DC. Tenochtitlan fu licenziato e distrutto i suoi monumenti. Dalle ceneri si levò la nuova capitale della colonia della Nuova Spagna e la lunga serie di civiltà mesoamericane che si erano estese fino all'Olmec arrivò a una fine drammatica e brutale.
La storia egiziana di Cenerentola smascherata › origini
Civiltà antiche
La storia di Cenerentola è una delle più popolari al mondo. In occidente, ha goduto di un seguito continuo dalla sua revisione e pubblicazione da Charles Perrault nel 1697 CE, ma la storia della giovane eroina, ingiustamente costretta a servitù, che diventa elevata ai reali fu raccontata per secoli prima in Cina durante la dinastia Tang (618-907 DC) nella storia di Yeh Shen.In questa storia la cattiva matrigna e la sorellastra uccidono gli amici animali di Yeh Shen ma alla fine vengono distrutti e la ragazza vince la mano del re.
La storia fu rielaborata nel XVII secolo in Italia, prima della versione di Perrault, dal poeta Giambattista Basile (1566-1632 dC). La pubblicazione postuma del famoso libro per bambini di Basile, Il Pentamerone, nel 1634 CE includeva la storia La Gatta Cenerentola (La cenerentola) che è riconosciuta come la prima apparizione europea della storia in stampa sebbene, come gli altri racconti di Basile, fosse già conosciuto in Italia. La storia è stata successivamente rielaborata e pubblicata in altre forme in Germania, Russia e altri paesi. La studiosa Particia Monaghan, che scrive sul racconto di Cenerentola, osserva:
La circolazione mondiale millenaria di Cenerentola rende la fiaba più conosciuta al mondo, ma nessuno può dire da dove inizia o quando le ciabatte magiche di Cenerentola l'hanno portata in Europa. (186)

Scarpetta di vetro
Un certo numero di autori moderni, tuttavia, in stampa e online, sostengono che la storia ha origine nell'antico Egitto e fornisce una versione che essi attribuiscono allo storico greco Strabone (65 BCE-23 CE). Tutti questi scrittori ripetono essenzialmente la stessa versione del racconto - che non assomiglia a Strabone - ma gli viene data autenticità dalla citazione di lui come fonte. Questi scrittori arrivano addirittura a citare "fatti" della storia antica che sostengono le loro affermazioni secondo cui il racconto popolare si basa su fatti reali e alcuni citano Erodoto o altre fonti antiche per dare più peso alle loro affermazioni.
LA STORIA DI CINDERELLA EGIZIANA GIORNATA MODERNA, RIPETUTA ATTUALMENTE CON PICCOLA VARIAZIONE ONLINE, È UN ESEMPIO DI COME LA RIPETIZIONE DIVENTA STORIA NELL'ERA DIGITALE.
In realtà, il racconto che continuano a presentare come "Cenerentola egiziana" non ha origini egiziane e, nella sua versione attuale, non appare da nessuna parte nella letteratura antica. La versione di Strabo della cosiddetta "Cenerentola egiziana" non ha quasi nessuno degli elementi della popolare versione moderna.
La proliferazione di siti e articoli che sostengono che la storia è un'opera egiziana non solo diffonde disinformazione ma è un cattivo servizio all'autore della storia che molto probabilmente ispira le loro affermazioni: Mrs Olive Beaupre Miller (1883-1968 CE) di Aurora, Illinois, Stati Uniti d'America. Miller ha brillantemente re-immaginato il racconto di Strabone, intrecciandolo con il racconto di Perrault, per creare un'antica Cenerentola egiziana e successivi scrittori, non avendo alcuna conoscenza di Miller o delle sue opere, ora presenta la storia come un vero racconto antico; in realtà ha meno di 100 anni.
ACCOUNT DI STRABO E ALTRE FONTI
Strabo racconta la storia nella sua geografia, libro XVII.33. L'account di Strabo è in realtà piuttosto breve. Racconta di come, durante un viaggio attraverso l'Egitto, abbia sentito una storia riguardante una cortigiana di nome Rhodopis per la quale è stata costruita la terza piramide di Giza. Lui scrive:
Raccontano la favolosa storia che, quando faceva il bagno, un'aquila strappò uno dei suoi sandali dalla sua cameriera e lo portò a Memphis ; e mentre il re stava amministrando la giustizia all'aria aperta, l'aquila, quando arrivò sopra la sua testa, gettò il sandalo sulle sue ginocchia; e il re, agitato sia dalla bella forma del sandalo che dalla stranezza dell'evento, mandò uomini in tutte le direzioni nel paese alla ricerca della donna che indossava il sandalo; e quando fu trovata nella città di Naucratis, fu allevata a Menfi [e] divenne la moglie del re.
Il racconto di Strabo, a differenza della versione attuale attribuita a lui, non include cattive "sorellastre" che perseguitano la cameriera, nessun maestro e nessuna festa; l'unico motivo della favola di Cenerentola è la "pantofola" usata per trovare la donna che sarà la moglie del re. L'uccello è anche chiaramente identificato come un'aquila che non era conosciuta in Egitto per gran parte della sua storia e appare in nessuna iconografia fino alla dinastia tolemaica (323-30 aC) e, anche in quel caso, non sarebbe stata l'uccello preferito in un antica storia egiziana.

Strabone
Strabo identifica la donna come Doricha che era l'amante del fratello di Saffo, Charaxus, e corregge Erodoto che si riferisce a lei come Rhodopis nelle sue storie II: 134. Doricha potrebbe essere stato il nome di nascita di Rhodopis (che significa "guance rosee" e probabilmente era un epiteto) o avrebbero potuto essere due donne diverse. Erodoto identifica Rhodopis come un Trace che fu venduto in schiavitù in Egitto e lavorò come cortigiana altamente pagata nella città di Naucratis, di proprietà dello stesso maestro che deteneva lo scrittore Esopo come schiavo. Il successivo scrittore Ateneo di Naucratis (III secolo dC) afferma che Rodopis e Doricha erano due donne diverse: Rhodopis era una cortigiana di grande bellezza mentre Doricha era una donna pia che faceva regolarmente offerte agli dei. Né Erodoto, Pre-Strabone, né Ateneo, più tardi, menzionano la storia dell'uccello e dei sandali. Lo storico Aelian (175-235 DC) ripete la storia di Strabo con qualche modifica nelle sue Storie varie XIII: 33, Sulla fortuna di Rodopi, una cortigiana :
Le relazioni degli egiziani affermano che Rhodopis era un cortigiano molto bello; e che in un momento mentre si stava facendo il bagno, Fortune, che ama fare cose stravaganti e inaspettate, le ha dato una ricompensa: sutable, non per la sua mente, ma per la sua bellezza. Per la più calda era la biancheria, e le sue domestiche le guardarono i vestiti, un'aquila chinandosi, afferrò una delle sue scarpe e la portò via a Memphis, dove Psammetichus era seduto in giudizio, e lasciò cadere la scarpa sulle sue ginocchia.. Psammetichus, meravigliandosi della forma della scarpa e della pulizia dell'opera, e dell'azione dell'uccello, inviato in tutto l'Egitto per scoprire la donna a cui apparteneva la scarpa; e dopo averla scoperta, l'ha sposata.
In questi antichi racconti, Rhodopis era una bella e costosa eterea, una cortigiana di molte abilità, e non sarebbe stata considerata un modello adatto per Olive Beaupre Miller nello scrivere letteratura per bambini. Miller, quindi, cambiò la cortigiana in una giovane fanciulla.
VERSIONE DI MILLER
Miller ha scritto la sua storia di Rhodopis come parte della sua casa editrice Bookhouse for Children e, anche se non ha tutti gli elementi del racconto finto-antico così popolare, sembra essere la fonte più immediata. Olive Beaupre Miller era una scrittrice che abbandonò le sue attività letterarie quando temeva che la distraessero dalla maternità. Si è dedicata a sua figlia, Virginia, ma era ancora interessata alla scrittura e alla letteratura. Quando non riusciva a trovare storie adatte a leggere a sua figlia, decise di crearne una sua. Joan Evanich, della Winnetka Historical Society, elabora:
Olive Beaupre Miller era costantemente alla ricerca di un'appropriata letteratura per bambini da leggere a sua figlia. Considerava le storie appropriate se rispondevano a tre criteri: dovevano essere scritte bene, formulare una dichiarazione etica positiva e essere classificate per adattarsi all'età evolutiva del bambino. Se non era in grado di trovare una storia o una poesia che soddisfacesse tutti e tre i requisiti, ne scrisse una lei stessa. (1)
Lei e suo marito hanno dato vita a una casa di pubblicazioni nota come Bookhouse for Children che pubblicava il tipo di storie che Miller riteneva appropriato per le giovani menti. Miller avrebbe incluso poesie di Emily Dickinson, Longfellow e prosa di altri scrittori ma, quando non riuscì a trovare una storia adatta a un certo volume, ne creò una che si sentiva adatta. Ha scritto la storia Rhodopis (The First Cinderella Story) per il volume di Bookhouse Through Fairy Halls pubblicato nel 1920 CE al fine di fornire al suo pubblico una storia affascinante che sapeva sarebbe stata popolare.
Nella prima pagina della storia, Miller scrive un disclaimer che afferma che la storia della regina Nitocris (che lei identifica come Rhodopis) è la più antica delle storie di Cenerentola e "fu raccontata ai bambini piccoli migliaia di anni prima di Cristo" (262). Nitocris, meglio conosciuto dalla storia raccontata da Erodoto ( Storie II.100 ) e menzionata da Manetho (III secolo aEV), non ha nulla a che vedere con la cortigiana Rhodopis. La storia di Erodoto racconta che Nitocris ha a che fare con la sua vendetta per l'omicidio di suo fratello, invitando i suoi assassini a un banchetto e poi annegandoli. Non è chiaro il motivo per cui Miller avrebbe affermato che queste due donne erano la stessa persona ma, a parte questo, non ci sono prove che la storia che lei racconta sia stata conosciuta migliaia di anni fa, né che "sia ancora una favola preferita in Egitto" (262). La storia è, infatti, la creazione stessa di Miller.
Miller ricrea brillantemente il breve resoconto dato da Strabone come una storia di una bella fanciulla egiziana il cui sandalo dorato è preso da un'aquila mentre sta facendo il bagno nel Nilo. L'azione della storia passa quindi al re sul suo trono, dispensando giustizia e mostrando misericordia a un contadino che non poteva pagare le sue tasse. Il re è abbattuto perché non ha moglie né famiglia quando, improvvisamente, l'aquila lascia cadere il sandalo sulle sue ginocchia.
Prendendo questo come un segno dagli dei, monta una ricerca nazionale per la fanciulla il cui piede si adatta al sandalo ma non riesce a trovarla. Il re è disperato perché crede di aver provato il sandalo ai piedi di ogni donna disponibile. A questo punto il contadino che ha risparmiato prima torna e dice al capo scriba del re che una bella fanciulla è stata trascurata. Poi dice loro dove Rhodopis si bagna la mattina e vanno a cercarla. Il piede di Rhodopis si adatta perfettamente al sandalo, naturalmente, e lei produce il suo compagno. Diventa la regina d'Egitto e la storia finisce felicemente.
Come per tutto il lavoro di Miller, la storia è raccontata con ritmo perfetto; ma non è un'antica favola egiziana. Ad un certo punto tra la sua pubblicazione nel 1920 CE e il presente, tuttavia, qualcuno lo revisionò in modo che diventasse la versione che si trova nelle pubblicazioni su Internet e altrove.
LA MODERNA "CITTÀ EGIZIANA"
La versione di questo racconto popolarmente conosciuta come "Egyptian Cinderella" trasforma molti degli elementi di Strabo, Aelian e Miller in una storia molto più elaborata. Qui, Rhodopis è una schiava povera, rapita dalla Grecia, che vive in Egitto in compagnia di altre donne schiave che la trattano male (le "sorellastre" del racconto di Cenerentola). È una persona gentile e longanime, una comunità di animali e lavora per un maestro gentile il cui grande piacere è fare un sonnellino sotto un albero preferito mentre i suoi schiavi si prendono cura della sua casa.
LA VERSIONE DI QUESTA RACCONTA POPOLARMENTE CONOSCIUTA COME LA "CINDERELLA EGIZIANA" TRASFORMA MOLTI ELEMENTI DI STRABO'S, AELIAN'S E MILLER IN UNA CACCIA MOLTO PIÙ ELABORATA.
Rhodopis è piuttosto aggraziata e un giorno il suo maestro la vede ballare mentre fa il suo lavoro ed è impressionata dal modo in cui sembra quasi planare da terra. Ha un paio di ciabatte meravigliosamente decorate che le regalano. Poco dopo, quando arriva la notizia che il faraone Amasis è in possesso di un grande festival, Rhodopis è entusiasta di partecipare e si immagina a ballare nelle sue belle scarpe. Le altre ragazze servite non le sono mai piaciute, e ora sono ancora più gelose del fatto che le sia stato mostrato un tale favore dal padrone. Le danno ancora più lavoro da fare e le dicono che non può partecipare al festival fino a quando tutto è completato. Rhodopis è al lavoro quando vede la barca del padrone salpare per i festeggiamenti con le altre ragazze a bordo.
Canta una canzone triste che sconvolge un vicino ippopotamo che si tuffa nel Nilo e bagna le sue pantofole. Rhodopis li mette su una roccia vicina ad asciugare quando una grande aquila (a volte data come falco o falco) piomba verso il basso e ne prende uno nei suoi artigli. La ragazza è sconvolta per la perdita ma mette la pantofola che ha lasciato nel suo vestito per la custodia e torna al suo lavoro.
Al festival, Amasis è seduta sul trono, annoiata e scoraggiata per la mancanza di una moglie, quando l'uccello lascia cadere la pantofola sulle sue ginocchia. Riconosce che questo è un segno del dio Horus e qualsiasi piede della fanciulla si adatta alla pantofola diventerà la sua regina. Ha ogni donna al festival che prova sulla pantofola ma nessuna è adatta.
Amasis, come il principe nel racconto di Cenerentola, attraversa poi il suo regno alla ricerca della ragazza il cui piede si adatta alla pantofola. Alla fine trova Rhodopis che non solo si adatta alla pantofola ma estrae il suo compagno dal suo vestito. La storia termina con Rhodopis, che presto diventerà regina, felicemente elogiata dal re in quanto le servitrici che erano così crudeli con lei devono tornare al loro lavoro.
Questa versione prende l'account di Miller e aggiunge i dettagli della trama che si trova nella storia di Cenerentola come è più noto: una povera ragazza trattata ingiustamente viene salvata dalla magia e elevata alla regina, mentre coloro che hanno abusato di lei soffrono.Si tratta chiaramente di una storia nata dalla favola di Cenerentola di Perrault e la "Cenerentola antica egiziana" di Miller, non dal racconto di Strabone. In sostenendo che la loro fonte per la storia è Strabone, gli scrittori devono affrontare in modo convincente con quattro obiezioni principali:
- conto di Strabone, come noto, non contiene la maggior parte degli elementi di questi scrittori includono.
- Non esiste una versione egiziana conosciuta della storia e non ha precedenti per questo tipo di storia nella letteratura egiziana. Dee sono spesso descritti come personaggi principali di leggende e racconti, non donne.
- Nessun altro scrittore fa menzione di questa particolare storia, anche se molti di riferimento una donna di grande bellezza di nome Rodopi e riferimento Strabone.
- La storia di una ragazza greca schiavo che diventa una regina d'Egitto non sarebbero stati ben accolto dalla cultura egiziana durante la maggior parte della sua storia.
Ripetizione come STORIA
Strabone scriveva nel 1 ° secolo dC durante la romana periodo della storia dell'Egitto che ha seguito la dinastia tolemaica. E 'possibile che qualche storia di una giovane schiava dalla Grecia, che ha sposato un re egiziano attraverso l'intervento divino, è stato detto durante il periodo tolemaico e questo è stato ripetuto Strabone. In tal caso, tuttavia, non v'è alcuna prova di esso. Strabone, Erodoto e altri tutti menzionano Rhodopris come legata al fratello della poetessa Saffo, raccontare la storia di come ha speso troppi soldi per comprare la sua libertà ed è stato castigato dalla sorella, e come lei era una donna di grande bellezza; ma nulla oltre le calzature che la lega a Cenerentola.
L'affermazione di scrittori moderni che la versione che presentiamo è un antico racconto egiziano primo registrato da Strabone è insostenibile come lo sono i "fatti" qualche utilità a sostegno della richiesta, come Rodopi come moglie noto di Amasi e l'uccello-e-pistone Motif così popolare nella letteratura egiziana. Non v'è alcuna traccia di una donna di nome Rodopi come moglie di Amasi I o Amasi e, mentre ci sono molti miti e leggende che caratterizzano gli animali egiziani, nessuno comprende un uccello consegnare una pantofola a un re.
La Cenerentola egiziano storia dei nostri giorni, attualmente ripetuto con piccole variazioni in linea, è un esempio di come la ripetizione si fa storia nell'era digitale. Come sempre più persone vengono a fare affidamento su informazioni digitali, meno tendono per controllare fonti primarie nei libri. Un articolo trovato on-line, la pretesa di essere la storia vera e propria, è accettato al valore nominale, semplicemente perché è stato trovato on-line e più siti ripetono le affermazioni di un articolo poi dare maggior peso. In questo caso, gli articoli costantemente citano Strabone come fonte, utilizzando esattamente la stessa frase senza elaborazione, mai citare il suo account originale, ma ancora la storia è accettato senza dubbio come un antico racconto dall'Egitto semplicemente perché lo scrittore dice che è.
Questo non è per dire che il racconto di Strabone aveva niente a che fare con lo sviluppo successivo della storia di Cenerentola. Forse quel singolo dettaglio di un re con un sandalo per trovare la sua regina ha ispirato il primo sconosciuto scrittore del racconto. Non è come se Strabone è stato uno scrittore oscura in alcun modo. Più tardi, nelle mani di un autore fantasioso come Olive Beaupré Miller, il racconto di Strabone prende vita ed è molto più convincente rispetto all'originale. Non si può affermare, tuttavia, che la versione attualmente così popolare è una prima versione egiziana di Cenerentola né che questa versione è stato impostato verso il basso da Strabone.
LICENZA
Articolo basato su informazioni ottenute da queste fonti:con il permesso dal sito web Ancient History Encyclopedia
Il contenuto è disponibile sotto Licenza Creative Commons: Attribution-NonCommercial-ShareAlike 3.0 Unported. Licenza CC-BY-NC-SA